Wide DHMPC DHMPCC

Decentralized and Hierarchical Model Predictive Control Class

This class implements the hierarchical MPC control approach presented in D. Barcelli, A. Bemporad, and G. Ripaccioli, [Hierarchical multi-rate control design for constrained linear systems in Proc. 49th IEEE Conf. on Decision and Control, Atlanta, GA, USA, 2010, pp. 5216–5221. and decentralized extension documented in D. Barcelli, A. Bemporad, and G. Ripaccioli, Decentralized hierarchical multi-rate control of constrained linear systems in Proc. 18th IFAC World Congress, Milano, Italy, 2011.

Assuming the plant stabilized by a linear lower level regulator, (e.g. obtained by means of DLRC) unable to enforce linear constraints on state and reference, this class computes restrictions on the reference that guarantees constraint satisfaction. Thus the user provided reference should be filtered so as to restrict both its magnitude and rate of variation, effectively imposing constraints on it. Then the class uses MPC, which is a constraint handling control scheme, for the supervisor layer (being it a single controller or a set of decentralized) and guarantee state constraint enforcement.

Introduction

In this work we propose a decentralized hierarchical multi-rate control design approach to linear systems subject to linear constraints on input and output variables. At the lower level, a set of linear controllers stabilize the open-loop process without considering the constraints. A higher-layer, composed of a set of independent controllers, commands reference signals at a lower sampling frequency so as to enforce linear constraints on the variables of the process. By optimally constraining the magnitude and the rate of variation of the reference signals applied to the lower control layer, we provide quantitative criteria for selecting the ratio between the sampling rates of the upper and lower layers to preserve closed-loop stability without violating the prescribed constraints.

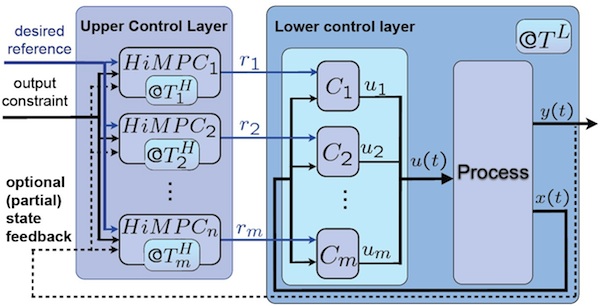
The HiMPC class has been developed to automatically generate the proposed multi-layer control architecture, which structure is shown in the following figure.

of the proposed approach. The decentralized design has been exploited together with the LTI model of the plant and the constraints on inputs and states to compute the polytopic sets of each submodel which is the bound the mutual influence of the different subsystems on each other. This result is fundamental because allows to treat each subsystem independently, since for all of them a single Maximal Output Admissible Set (MOAS) is computed [1]. The independece of the MOASs is guaranteed by taking into account the uncertainty polytope, which bounds the interaction with the others, in the invariant set computation.

Moreover, the MOAS determination is related to the restriction of the admissible output set, which is a polytope tightening. The contraction factor, Δk, is the main tuning knob of the approach: the smaller the components of Δk, the larger is the set of admissible set points, but the smaller will be the admissible reference increments to maintain tracking errors within the admissible error set.

Such control architecture is then extended to allow a decentralized superviros which is then capable of speedup the sampling frequencies in those spatial regiogion presenting less strict challanges. Cooperativeness is avoided to guarantee complete independece, a clear advantage from communication and parallelism viewpoints. So as to achieve this, inter-subsystem interractions are treated as disturbances, leading to consider Maximal Output Admissible Robust Set (MOARS) instead of MOAS.

Then for each subsystem, the maximum element-wise reference variation such that for any admissible state and interaction, the system state will be in a MOAS at the next execution of higher level controller. It is evident that such variation is a function of the ratio between the two layers sample time. The constraint computed in that way bounds the reference variation that is possible to give to the sub-controllers, while preserving the closed-loop stability and enforcing the constraints. Such task is performed by the higher level controllers.

Finally the maximum element-wise reference variation for each subsystem is computed. The maximum element-wise reference variation is defined as the smallest change of reference vector that can be applied to the closed-loop system of the lower layer controllers with the plant such that, starting from an invariant set, the state vector lands outside a new invariant set a given number of steps. Or, in other words, for all reference changes the closed-loop system is such that, starting from an invariant set, the state vector always arrives into a new invariant set after given number of steps.

[1] Kolmanovsky, I. and Gilbert, E.G., Maximal output admissible sets for discrete-time systems with disturbance inputs, 14th American Control Conference 1995, Seattle, WA

Theoretical background

yet to be done

Class Description

Public Properties

• DeltaK : Array of the same size of the constraints that determines their tightening
• Xcon : Structure of constraints with fields
  • min;
  • max;
• dec : Decentralization structure, is a cell array of structures each of which with fileds:
  • x (states of the subsystem);
  • y (outputs of the subsystem);
  • u (inputs of the subsystem);
  • applied (inputs effectively applied, no overlap is allowed).
• model : ss object with the plant LTI model
• comp : Cell array of the state indices that the do not belong to the i-th subsystem
• coupledCons: Cell array of non element-wise state constraints with fields H and K to be appended to the constraint polytope of the i-th subsystem.

Class Methods

Class Contructor obj = HiMPC(model,dec,Ycon,DeltaK,Xcon,coupledCons)

• model : ss object with the plant LTI model
• dec : Decentralization structure array of structures with fields:
  • x (states of the subsystem);
  • y (outputs of the subsystem);
  • u (inputs of the subsystem);
  • applied (inputs effectively applied, no overlap is allowed).
• DeltaK : Array of the same size of the constraints that determines their tightening
• Xcon : state bounds structure eight fields min and max
• coupledCons: Cell array of non element-wise state constraints with fields H and K to be appended to the constraint polytope of the corresponding subsystem

MOARS computation obj=computeMOARS(obj) Computes the MOARS for all subsystems.

MOARS plot obj=plotMOARS(obj) Plot the MOARS of each subsystem along with the corresponding MOAS (which neglects interactions with the rest for the plant, hence disturbances). Meaningful plot can be obtained for objects lying at most in three dimensional spaces.

Compute DeltaR and DeltaR/N"" obj=computeDeltaR(obj) Computes the maximum reference variation of each sub-model as a function of the sample time ratio, also with sample time normalization.

Plot DeltaR and DeltaR/N obj=plotDeltaR(obj) Creates two figures with as many subfigures as subsystems, in which Δ_r(N) and Δ_r(N) / N are shown, respectively, as functions for the upper-lower layer sample time ratio N

[Wide Main Page]