SGRN main
Contents |
GODEL Gene ordinary differential equation library
In GODEL, the evolution of gene product concentrations is assumed to be governed by Boolean-Like ODE models that are briefly introduced below. We also provide a simple example illustrating the main features of GODEL.
Boolean-like models of genetic regulatory networks
In the context of Boolean
networks, the activation status of gene i, with 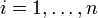 ,
is encoded by a binary variable Xi that is 1 if the gene
is active and 0 otherwise. The laws governing the
activation of gene i are captured by a Boolean rule
,
is encoded by a binary variable Xi that is 1 if the gene
is active and 0 otherwise. The laws governing the
activation of gene i are captured by a Boolean rule
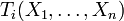 . In practice, Ti depends only on the
subset of variables
. In practice, Ti depends only on the
subset of variables 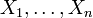 corresponding to the genes
that control the expression of gene i.
corresponding to the genes
that control the expression of gene i.
For defining quantitative dynamics of gene expression that incorporate the logical structure of Boolean networks, we follow an approach inspired by [1] and
consider ODE models of the form
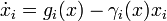
where 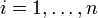 denotes the i-th of n genes,
denotes the i-th of n genes,
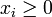 denotes the concentration of the corresponding product,
denotes the concentration of the corresponding product, 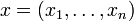 ,
,
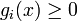 is a synthesis rate and
is a synthesis rate and 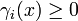 is a degradation function.
is a degradation function.
In order to account for the discrete regulatory logics, functions bi(x) and γi(x) are typically a combination of switch-like (e.g. sigmoidal) regulatory functions describing the effect of protein j on the expression of gene i and the synthesis of the corresponding protein.
According to [1], each variable Xi is replaced by a monotone, nondecreasing sigmoidal function
![\sigma^+:[0,+\infty)\to [0,1]](/HYCON2/images/math/d/3/5/d35bd37ffb98f0ee1a13fae8566c1f05.png) of the concentration xi. Given any two functions τ(x) and τ'(x) representing the
Boolean expressions T(x) and T'(X),
of the concentration xi. Given any two functions τ(x) and τ'(x) representing the
Boolean expressions T(x) and T'(X), 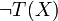 is replaced by 1 − τ(x) and
is replaced by 1 − τ(x) and 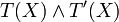 by
by 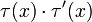 . In particular,
. In particular, 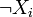 is represented by σ − (xi) = 1 − σ + (xi).
is represented by σ − (xi) = 1 − σ + (xi).
As an example, b(x) = σ + (x1)σ − (x2) and 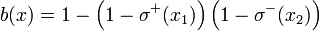 correspond to the Boolean formulas
correspond to the Boolean formulas 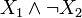 and
and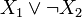 , respectively.
, respectively.
Further details on this class of models can be found in [2], [3] and [4].
GODEL features
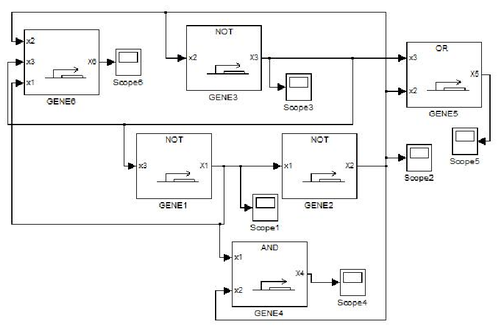
GODEL offers pre-defined functions for sigmoids commonly used for modelling gene dynamics, namely Hill's function and piecewise multi-affine functions. The main advantage of GODEL is that building a model of a genetic network only amounts to introduce a GODEL block for each gene and connections among regulated genes. The resulting schemes are very similar to networks drawn by hand and this considerably ease the debugging of complex models. As an example, the following genetic network
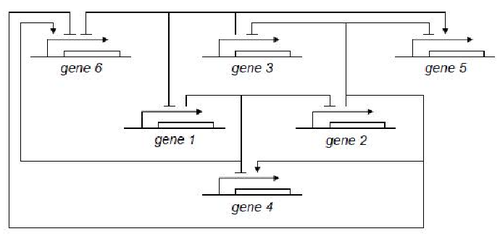
corresponds to the GODEL model
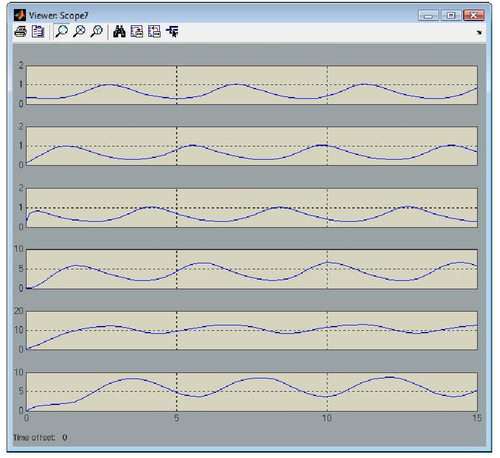
One can notice that to each gene corresponds a gene block that is available from the GODEL library. Furthermore, GODEL offers the possibility of specifying arbitrary regulation functions bi and γi (as it as been done for gene 6, that depends upon three regulators) as well as of using pre-defined blocks corresponding to the basic Boolean functions AND, OR and NOT (see, e.g., genes 4,5 and 1). Simulation of gene-product concentrations starting from suitable initial concentrations can be done in one click so obtaining the following concentration profiles