ABB_CC_Testcase.TwoNode

Information

'Mini' benchmark problem with detailed equation-based modelling

Name	Description
OpenLoop	Open loop power system
OpenLoopEq	Open loop power system, modelled using equations
PrimaryController	Primary Control System
PrimaryControlledSystem	System with primary controllers connected
ClosedLoop	Connection of OpenLoop and Primary control systems with no secondary control.
ClosedLoop2	Connection of OpenLoop and Primary with secondary control.
NoControl	TwoNode TestCase without primary controls
ShedRelay
SimplePrimaryController	Primary Control System
SimplePrimaryControlledSystem
ComparePrimaryControls
OpenLoopIndexReduced
VerifyIdxReduced

ABB_CC_Testcase.TwoNode.OpenLoop

Information

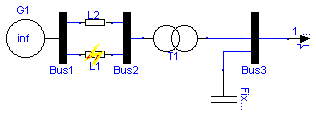
Model of the Open Loop mini test case built using the standard component library.

Modelica definition

model OpenLoop "Open loop power system" 
  Components.Slack G1(V0=1.05504739284515);
  Components.Bus Bus1;
  Components.Varimp L1;
  Components.Impedance L2(X=0.5);
  Components.Bus Bus2;
  Components.Bus Bus3;
  ABB_CC_Testcase.Components.Transformer T1(X=1e-9);
  input Integer LoadStep;
  input Integer TapStep;
  ABB_CC_Testcase.Components.FixCapacitor FixCapacitor1(B=0.2);
  Components.Load Load(P0=1, Q0=0.3);
equation 
  //  L1.X = if time > 20 then Modelica.Constants.inf else 0.5;
  L1.X = if time > 10 then 1e5 else 0.5;
  Load.step = LoadStep;
  T1.tappos = TapStep;
  
  connect(G1.T, Bus1.T);
  connect(L2.T1, G1.T);
  connect(L1.T2, G1.T);
  connect(Bus2.T, T1.T1);
  connect(T1.T2, Bus3.T);
  connect(FixCapacitor1.T, Bus3.T);
  connect(L1.T1, Bus2.T);
  connect(L2.T2, Bus2.T);
  connect(Load.T, Bus3.T);
end OpenLoop;

ABB_CC_Testcase.TwoNode.OpenLoopEq

Information

Model of the Open Loop mini test case built using direct mathematical modelling.
This model is equivalent to OpenLoop.

Parameters

Name	Default	Description
v0	1.05504739284515
P0	1
Q0	0.3
B0	0.2
as	0
at	2
bs	0
bt	2
Tp	60
Tq	60
faultTime	10

Modelica definition

model OpenLoopEq "Open loop power system, modelled using equations" 
  // parameters
  parameter Real v0=1.05504739284515;
  parameter Real P0=1;
  parameter Real Q0=0.3;
  parameter Real B0=0.2;
  parameter Real as=0;
  parameter Real at=2;
  parameter Real bs=0;
  parameter Real bt=2;
  parameter Real Tp=60;
  parameter Real Tq=60;
  parameter Real faultTime=10;
  
  output Real x[2]={xp,xq};
  output Real y[2](start={1,0}) = {v,delta};
  input Real u[3]={n,k,X};
  // variables
  Real xp;
  Real xq;
  Real v(start=1);
  Real delta;
  Real k;
  Real n;
  Real X;
equation 
  // vector versions
  {der(xp),der(xq)} = {(-xp/Tp + P0*(v^as - v^at)),(-xq/Tq + Q0*(v^bs - v^bt))};
  
  {0,0} = {v*sin(delta)*v0/(X*n) + (1 - k)*(xp/Tp + P0*v^at),-(v0*v*cos(delta))
    /(n*X) + v^2/(n^2*X) - B0*v^2 + (1 - k)*(xq/Tq + Q0*v^bt)};
initial equation 
  der(xp) = 0;
  der(xq) = 0;
end OpenLoopEq;

ABB_CC_Testcase.TwoNode.PrimaryController

Information

This model models the primary control systems of the 
four node power system. 
It contains a tap changer controller for transformer T1
modelled as a state machine and an automatic voltage regulator
with filed voltage limiter modelled by a state machina and a linear 
control law.
The special equations activated by the flag SimulinkSafe
flag are jus fixes that must be applied to make the model simulable with
Simulink. If you remodel this system with other tools,
use the original equations (assume that SimulinkSafe=false)

Parameters

Name	Default	Description
idle0	false
wait0	true
action0	false
tappos0	0
timer0	0
up_limit0	false
TapDelay	30
MechDelay	1
TapDB	0.01*3
MaxTap	10
MinTap	-10

Modelica definition

model PrimaryController "Primary Control System" 
  parameter Boolean idle0=false;
  parameter Boolean wait0=true;
  parameter Boolean action0=false;
  parameter Integer tappos0=0;
  parameter Real timer0=0;
  parameter Boolean up_limit0=false;
  
  input Real TapVref(start=1);
  input Real v(start=1);
  
  Boolean idle(start=idle0, fixed=true);
  Boolean wait(start=wait0, fixed=true);
  Boolean action(start=action0, fixed=true);
  Integer tappos(start=tappos0, fixed=true);
  Real timer(start=timer0, fixed=true);
  
  Boolean toohigh;
  Boolean toolow;
  
  output Integer T1tappos;
  
  parameter Real TapDelay=30;
  parameter Real MechDelay=1;
  parameter Real TapDB=0.01*3;
  parameter Real MaxTap=10;
  parameter Real MinTap=-10;
  
equation 
  T1tappos = pre(tappos);
  // tap changer control - state automata !
  toohigh = (v - TapVref) > TapDB/2;
  toolow = (v - TapVref) < -TapDB/2;
  
  idle = (pre(idle) or pre(wait)) and not (toohigh or toolow) or (pre(action)
     and ((time - timer) > TapDelay + MechDelay));
  wait = (pre(idle) and (toohigh or toolow)) or pre(wait) and ((toolow or 
    toohigh) and ((time - pre(timer)) < TapDelay));
  action = (pre(wait) and (time - timer > TapDelay)) or pre(action) and ((time
     - timer) < TapDelay + MechDelay);
  when wait and not pre(wait) and not initial() then
    timer = time;
  end when;
  when pre(action) and not action then
    if toolow and (pre(tappos) < MaxTap) then
      tappos = pre(tappos) + 1;
    elseif toohigh and (pre(T1tappos) > MinTap) then
      tappos = pre(tappos) - 1;
    else
      tappos = pre(tappos);
    end if;
  end when;
end PrimaryController;

ABB_CC_Testcase.TwoNode.PrimaryControlledSystem

Information

Connection of OpenLoop and Primary control systems

Parameters

Name	Default	Description
faultTime	10
tapstepsize	0.02
loadstepsize	0.05

Modelica definition

model PrimaryControlledSystem 
  "System with primary controllers connected" 
  ABB_CC_Testcase.TwoNode.OpenLoopEq System;
  ABB_CC_Testcase.TwoNode.PrimaryController PrimCon;
  parameter Real faultTime=10;
  parameter Real tapstepsize=0.02;
  parameter Real loadstepsize=0.05;
  
  input Real LoadStep;
equation 
  System.u = {1 + tapstepsize*PrimCon.T1tappos,LoadStep*loadstepsize,if time > 
    faultTime then 0.5 else 0.25};
  PrimCon.v = System.v;
  PrimCon.TapVref = 1;
end PrimaryControlledSystem;

ABB_CC_Testcase.TwoNode.ClosedLoop

Information

Connection of OpenLoop and Primary control systems with no secondary control.

Modelica definition

model ClosedLoop 
  "Connection of OpenLoop and Primary control systems with no secondary control."
   
  
  ABB_CC_Testcase.TwoNode.PrimaryControlledSystem System(faultTime=90);
equation 
  System.LoadStep = 0;
end ClosedLoop;

ABB_CC_Testcase.TwoNode.ClosedLoop2

Information

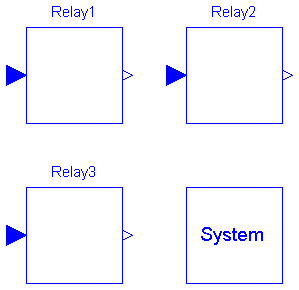
Connection of OpenLoop and Primary control systems with secondary control using
undervoltage load shedding relays.

Modelica definition

model ClosedLoop2 
  "Connection of OpenLoop and Primary  with  secondary control." 
  ShedRelay Relay1(
    Threshold=.8, 
    DelayTime=1.5, 
    ShedAmount=.05);
  ShedRelay Relay2(
    Threshold=.82, 
    DelayTime=3, 
    ShedAmount=.05);
  ShedRelay Relay3(
    DelayTime=6, 
    ShedAmount=0.05, 
    Threshold=.92);
equation 
  Relay1.inPort.signal[1] = System.System.v;
  Relay2.inPort.signal[1] = System.System.v;
  Relay3.inPort.signal[1] = System.System.v;
  System.System.k = Relay1.y + Relay2.y + Relay3.y;
public 
  ABB_CC_Testcase.TwoNode.PrimaryControlledSystem System;
end ClosedLoop2;

ABB_CC_Testcase.TwoNode.NoControl

Information

This is a model of the twonode testcase, where no primary control systems has been connected.
Instead the tap ratio is fixed at 1 p.u. and the load shedding input at 0 p.u.
A fault on the the line is modelled of the change of the line impedance from 0.25 to 0.5 p.u. at
time 10 s.

Parameters

Name	Default	Description
faultTime	30

Modelica definition

model NoControl "TwoNode TestCase without primary controls" 
  parameter Real faultTime=30;
  ABB_CC_Testcase.TwoNode.OpenLoopEq System;
equation 
  System.u = {1,0,if time > faultTime then 0.5 else 0.25};
end NoControl;

ABB_CC_Testcase.TwoNode.ShedRelay

Information

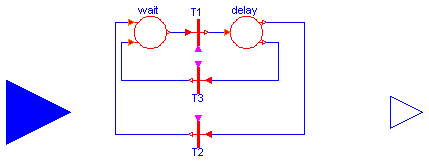
Standard load shedding relay.

Parameters

Name	Default	Description
Threshold	0.95
DelayTime	1
ShedAmount	0.05

Modelica definition

class ShedRelay 
  extends Modelica.Blocks.Interfaces.SISO;
  parameter Real Threshold=0.95;
  parameter Real DelayTime=1;
  
  parameter Real ShedAmount=0.05;
  discrete Real timerstart(start=-1, fixed=true);
  
  ModelicaAdditions.PetriNets.Transition T1;
  ModelicaAdditions.PetriNets.Transition T2;
  ModelicaAdditions.PetriNets.Place12 delay;
  ModelicaAdditions.PetriNets.Transition T3;
  ModelicaAdditions.PetriNets.Place21 wait(initialState=true);
equation 
  connect(delay.inTransition, T1.outTransition);
  connect(T3.inTransition, delay.outTransition1);
  connect(delay.outTransition2, T2.inTransition);
  connect(T1.inTransition, wait.outTransition);
  connect(T2.outTransition, wait.inTransition2);
  connect(T3.outTransition, wait.inTransition1);
  
  T1.condition = (u < Threshold) and (y < ShedAmount/10);
  T2.condition = (u > Threshold);
  T3.condition = time > timerstart + DelayTime;
  
  when delay.state then
    timerstart = time;
  end when;
  
  when T3.condition and delay.state then
    outPort.signal[1] = ShedAmount;
  end when;
initial equation 
  wait.state = true;
  delay.state = false;
  y = 0;
end ShedRelay;

ABB_CC_Testcase.TwoNode.SimplePrimaryController

Information

This model models the primary control systems of the 
four node power system using a simplified discrete-time approximation.

Parameters

Name	Default	Description
tappos0	0
up_limit0	false
TapDelay	30
MechDelay	1
TapDB	0.01*3
MaxTap	10
MinTap	-10

Modelica definition

model SimplePrimaryController "Primary Control System" 
  parameter Integer tappos0=0;
  parameter Boolean up_limit0=false;
  
  input Real TapVref(start=1);
  input Real v(start=1);
  
  Integer tappos(start=tappos0, fixed=true);
  
  Boolean toohigh;
  Boolean toolow;
  
  output Integer T1tappos;
  
  parameter Real TapDelay=30;
  parameter Real MechDelay=1;
  parameter Real TapDB=0.01*3;
  parameter Real MaxTap=10;
  parameter Real MinTap=-10;
  
equation 
  when sample(0, TapDelay + MechDelay) then
    // tap changer control - simple discrete implementation
    toohigh = (v - TapVref) > TapDB/2;
    toolow = (v - TapVref) < -TapDB/2;
    if toolow and (pre(tappos) < MaxTap) then
      tappos = pre(tappos) + 1;
    elseif toohigh and (pre(T1tappos) > MinTap) then
      tappos = pre(tappos) - 1;
    else
      tappos = pre(tappos);
    end if;
  end when;
  T1tappos = pre(tappos);
end SimplePrimaryController;

ABB_CC_Testcase.TwoNode.SimplePrimaryControlledSystem

Parameters

Name	Default	Description
faultTime	10
tapstepsize	0.02
loadstepsize	0.05

Modelica definition

model SimplePrimaryControlledSystem 
  ABB_CC_Testcase.TwoNode.OpenLoopEq System;
  ABB_CC_Testcase.TwoNode.SimplePrimaryController PrimCon;
  parameter Real faultTime=10;
  parameter Real tapstepsize=0.02;
  parameter Real loadstepsize=0.05;
  
  input Real LoadStep;
equation 
  System.u = {1 + tapstepsize*PrimCon.T1tappos,LoadStep*loadstepsize,if time > 
    faultTime then 0.5 else 0.25};
  PrimCon.v = System.v;
  PrimCon.TapVref = 1;
end SimplePrimaryControlledSystem;

ABB_CC_Testcase.TwoNode.ComparePrimaryControls

Modelica definition

model ComparePrimaryControls 
  ABB_CC_Testcase.TwoNode.SimplePrimaryControlledSystem SimpleSystem;
  ABB_CC_Testcase.TwoNode.PrimaryControlledSystem System;
equation 
  System.LoadStep = 0;
  SimpleSystem.LoadStep = 0;
end ComparePrimaryControls;

ABB_CC_Testcase.TwoNode.OpenLoopIndexReduced

Information

Model of the Open Loop mini test case built using direct mathematical modelling.
This model is equivalent to OpenLoop.

Parameters

Name	Default	Description
v0	1.05504739284515
P0	1
Q0	0.3
B0	0.2
as	0
at	2
bs	0
bt	2
Tp	60
Tq	60
faultTime	10

Modelica definition

model OpenLoopIndexReduced 
  // parameters
  parameter Real v0=1.05504739284515;
  parameter Real P0=1;
  parameter Real Q0=0.3;
  parameter Real B0=0.2;
  parameter Real as=0;
  parameter Real at=2;
  parameter Real bs=0;
  parameter Real bt=2;
  parameter Real Tp=60;
  parameter Real Tq=60;
  parameter Real faultTime=10;
  
  output Real x[2]={xp,xq};
  output Real y[2](start={1,0}) = {v,delta};
  input Real u[3]={n,k,X};
  
  Real[2, 2] gx;
  Real[2, 2] gy;
  Real[2, 1] f;
  Real[2, 1] g;
  Real[2, 2] invgy;
  
  // variables
  Real xp;
  Real xq;
  Real v(start=1);
  Real delta;
  Real k;
  Real n;
  Real X;
equation 
  // vector versions
  f = [-xp/Tp + P0*(v^as - v^at); -xq/Tq + Q0*(v^bs - v^bt)];
  [der(xp); der(xq)] = f;
  g = [v*sin(delta)*v0/(X*n) + (1 - k)*(xp/Tp + P0*v^at); -(v0*v*cos(delta))/(n
    *X) + v^2/(n^2*X) - B0*v^2 + (1 - k)*(xq/Tq + Q0*v^bt)];
  
  gx = [(1 - k)/Tp, 0; 0, (1 - k)/Tq];
  gy = [sin(delta)*v0/X/n + (1 - k)*P0*v^at*at/v, v0*v*cos(delta)/X/n; -v0*cos(
    delta)/X/n + 2*v/n^2/X - 2*B0*v + (1 - k)*Q0*v^bt*bt/v, v*sin(delta)*v0/X/n];
  
  invgy = [v*sin(delta)*X*n^2/(sin(delta)^2*n*v0*v - sin(delta)*n^2*P0*v^at*at*
    X*k + sin(delta)*n^2*P0*v^at*at*X + v0*cos(delta)^2*n*v - 2*cos(delta)*v^2
     + 2*cos(delta)*B0*v^2*X*n^2 + cos(delta)*Q0*v^bt*bt*X*n^2*k - cos(delta)*
    Q0*v^bt*bt*X*n^2), -v*cos(delta)*X*n^2/(sin(delta)^2*n*v0*v - sin(delta)*n^
    2*P0*v^at*at*X*k + sin(delta)*n^2*P0*v^at*at*X + v0*cos(delta)^2*n*v - 2*
    cos(delta)*v^2 + 2*cos(delta)*B0*v^2*X*n^2 + cos(delta)*Q0*v^bt*bt*X*n^2*k
     - cos(delta)*Q0*v^bt*bt*X*n^2); (v0*cos(delta)*n*v - 2*v^2 + 2*B0*v^2*X*n^
    2 + Q0*v^bt*bt*X*n^2*k - Q0*v^bt*bt*X*n^2)*X*n/v/v0/(sin(delta)^2*n*v0*v - 
    sin(delta)*n^2*P0*v^at*at*X*k + sin(delta)*n^2*P0*v^at*at*X + v0*cos(delta)
    ^2*n*v - 2*cos(delta)*v^2 + 2*cos(delta)*B0*v^2*X*n^2 + cos(delta)*Q0*v^bt*
    bt*X*n^2*k - cos(delta)*Q0*v^bt*bt*X*n^2), -(-sin(delta)*v0*v + P0*v^at*at*
    X*n*k - P0*v^at*at*X*n)*X*n^2/v/v0/(sin(delta)^2*n*v0*v - sin(delta)*n^2*P0
    *v^at*at*X*k + sin(delta)*n^2*P0*v^at*at*X + v0*cos(delta)^2*n*v - 2*cos(
    delta)*v^2 + 2*cos(delta)*B0*v^2*X*n^2 + cos(delta)*Q0*v^bt*bt*X*n^2*k - 
    cos(delta)*Q0*v^bt*bt*X*n^2)];
  
  //   [0; 0] = g;
  //  [der(v); der(delta)] = -invgy*gx*f;
  [0; 0] = gx*f + gy*[der(v); der(delta)];
initial equation 
  gx*f = [0; 0];
  g = [0; 0];
  
end OpenLoopIndexReduced;

ABB_CC_Testcase.TwoNode.VerifyIdxReduced

Modelica definition

model VerifyIdxReduced 
  OpenLoopIndexReduced OpenLoopIndexReduced1;
equation 
  OpenLoopIndexReduced1.u = {1,0,if time > 10 then 0.5 else 0.25};
end VerifyIdxReduced;