ABB_CC_Testcase.Components

Information

Component models used for the different test cases

Name	Description
Slack	Slack Node
Gen3	3rd Order Detailed Generator
Load	Dynamic exponential recovery load
GenQSS	Quasi-Steady State Model of a generator
Transformer	Transformer with Voltage Controller
Varimp
Capacitor
IdealTransformer
ImpTransformer
Basic
Bus	Busbar model
Impedance	Impedance model
Pilink	Pilink Line Model
GenQSS2	Quasi-Steady State Model of a generator
FixCapacitor
FixTransformer	Fixed Ratio Transformer
LinearRecoveryLoad	Dynamic exponential recovery load
ParTripLine
SimplerLoad	ZIP recovery load
DBControl	Integral controller with Deadband

ABB_CC_Testcase.Components.Slack

Information

The slack node model acts as slack bus in initialization or load-flow 
calculations and as an infinite bus during dynamic simulation. 
In addition it defines the reference for the phasor calculation.

Parameters

Name	Default	Description
V0	1
theta0	0

Modelica definition

model Slack "Slack Node" 
  extends Basic.OnePin;
  
  parameter Real V0=1;
  parameter Real theta0=0;
  Real Pg;
  Real Qg;
equation 
  
  1 + T.va = V0*cos(theta0);
  T.vb = V0*sin(theta0);
  Pg = -((1 + T.va)*T.ia + T.vb*T.ib);
  Qg = -(T.vb*T.ia - (1 + T.va)*T.ib);
  
end Slack;

ABB_CC_Testcase.Components.Gen3

Information

The 3rd order detailed generator model corresponds to Model 3 in [1, pp 348],
and extends the DetGen class. It adds a single transient EMF source in
the quatradure axis and the field voltage input. This model neglects the effect
of damper windings and the damping produced by rotor eddy-currents.
The effect of this damping is usually included in the damping coefficient D.
Each generator has it's own dq coordinate system, and its stator equations
must therefore be related to the network (global) coordinate system using the
so called Kron's transformations [1, pp. 90].
---
[1] J. Machowski, J.W. Bialek, and J.R. Bumby, Power System Dynamics and
Stability, Number ISBN 0-471-97174. Wiley, 1993.

Parameters

Name	Default	Description
H	3	Inertia Constant
D	0	Damping Coefficient
ra	0	Armature Resistance
xd	0.8948	Direct Axis Synchronous Reactance
xq	0.84	Quadrature Axis Synchronous Reactance
xdp	0.30	Direct Axis Transient Reactance
Td0p	7	Open-circuit Direct Axis Transient Time Constant
Ef0	1.72250079258051
Efmax	2.2
Pm0	0.352
Pmmax	1
wref	1

Modelica definition

model Gen3 "3rd Order Detailed Generator" 
  extends Basic.OnePin;
  parameter Real H=3 "Inertia Constant";
  parameter Real D=0 "Damping Coefficient";
  
  parameter Real ra=0 "Armature Resistance";
  parameter Real xd=0.8948 "Direct Axis Synchronous Reactance";
  parameter Real xq=0.84 "Quadrature Axis Synchronous Reactance";
  parameter Real xdp=0.30 "Direct Axis Transient Reactance";
  parameter Real Td0p=7 "Open-circuit Direct Axis Transient Time Constant";
  
  parameter Real Ef0=1.72250079258051;
  parameter Real Efmax=2.2;
  
  parameter Real Pm0=0.352;
  parameter Real Pmmax=1;
  parameter Real wref=1;
  
  input Real Vref;
  
  Real Eqp(start=1);
  Real w(start=1) "Angular Speed";
  Real delta "Rotor Angle";
  
  Real id;
  Real iq "dq Armature Current";
  Real vd;
  Real vq "dq Armature Voltage";
  Real Pe;
  
  Real Efd;
  Real dEfd;
  Real Pm;
  Real dPm;
  Real V;
  
equation 
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
  
  //   swing equations
  der(w) = 1/(2*H)*(Pm - Pe - D*(w - 1));
  der(delta) = 2*Modelica.Constants.PI*50*(w - 1);
  
  // Transient EMF equation
  Td0p*der(Eqp) = Efd - Eqp + id*(xd - xdp);
  
  // stator equations
  vd = -ra*id - xq*iq;
  vq = Eqp + xdp*id - ra*iq;
  
  // electrical power
  Pe = Eqp*iq + (xdp - xq)*id*iq;
  
  // coordinate change
  -T.ia = -sin(delta)*id + cos(delta)*iq;
  -T.ib = cos(delta)*id + sin(delta)*iq;
  1 + T.va = -sin(delta)*vd + cos(delta)*vq;
  T.vb = cos(delta)*vd + sin(delta)*vq;
  
  // generator voltage control
  2.5*der(dEfd) + dEfd = 50*(Vref - V);
  Efd = min(Efmax, dEfd + Ef0);
  // governor control
  10*der(dPm) + dPm = 1.5*(wref - w);
  Pm = min(Pmmax, dPm + Pm0);
end Gen3;

ABB_CC_Testcase.Components.Load

Information

Dynamic exponential recovery load according to Karlsson 
The load powers are given by:
  der(xp) = P0*(V^(as) - V^at) - xp/Tp;
  Pl = (xp/Tp + P0*V^at);
  der(xq) = Q0*(V^(bs) - V^bt) - xq/Tq;
  Ql = (xq/Tq + Q0*V^bt);
where xp is a continuous dynamic state that can be interpreted as a
measure of the energy deficit in the load and Ps(V) = P0*V^as 
is the steady-state and Pt(V)=P0*V^at the transient voltage dependency.
Pl is the actual active load power and Tp is the active power recovery 
time constant. 
For the reactive load power, a similar model is used with corresponding 
characteristics x_q, Qs(V)=Q0 V^bs, Qt(V) = Q0 V^bt and time constant Tq.
---
[1] D. Karlsson and D.J. Hill, "Modelling and identification of nonlinear 
dynamic loads in power systems", IEEE Transactions on Power Systems, 
vol. 9, no. 1, pp. 157-163, February 1994.

Parameters

Name	Default	Description
xp0	0	Initial Value for xp
xq0	0	Initial Value for xq
P0	.1	Rated Active Power Load
Q0	.02	Rated Reactive Power Load
as	0	Steady-state active power voltage dependency
at	2	Transient active power voltage dependency
bs	0	Steady-state reactive power voltage dependency
bt	2	Transient reactive power voltage dependency
Tp	60	Active power recovery time constant
Tq	60	Reactive power recovery time constant
ShedStep	0.05

Modelica definition

model Load "Dynamic exponential recovery load" 
  extends Basic.OnePin;
  parameter Real xp0=0 "Initial Value for xp";
  parameter Real xq0=0 "Initial Value for xq";
  parameter Real P0=.1 "Rated Active Power Load";
  parameter Real Q0=.02 "Rated Reactive Power Load";
  parameter Real as=0 "Steady-state active power voltage dependency";
  parameter Real at=2 "Transient active power voltage dependency";
  parameter Real bs=0 "Steady-state reactive power voltage dependency";
  parameter Real bt=2 "Transient reactive power voltage dependency";
  parameter Real Tp=60 "Active power recovery time constant";
  parameter Real Tq=60 "Reactive power recovery time constant";
  parameter Real ShedStep=0.05;
  discrete input Integer step(min=0, max=3) "Load Shedding Constant";
  Real xp(
    min=-1, 
    max=1, 
    start=xp0, 
    fixed=true) "Internal Load State";
  Real xq(
    min=-1, 
    max=1, 
    start=xq0, 
    fixed=true) "Internal Load State";
  Real V;
  Real Pl;
  Real Ql;
equation 
  Pl = (1 - step*ShedStep)*(xp/Tp + P0*V^at);
  Ql = (1 - step*ShedStep)*(xq/Tq + Q0*V^bt);
  der(xp) = P0*(V^as - V^at) - xp/Tp;
  der(xq) = Q0*(V^bs - V^bt) - xq/Tq;
  
  T.ia = (T.vb*Ql + Pl + Pl*T.va)/(1 + 2*T.va + T.va*T.va + T.vb*T.vb);
  T.ib = (Pl*T.vb - Ql - T.va*Ql)/(1 + 2*T.va + T.va*T.va + T.vb*T.vb);
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
end Load;

ABB_CC_Testcase.Components.GenQSS

Information

This model neglects the electromechanical dynamics of the
generator. 

Parameters

Name	Default	Description
H	3	Inertia Constant
D	0	Damping Coefficient
ra	0	Armature Resistance
xd	0.8948	Direct Axis Synchronous Reactance
xq	0.84	Quadrature Axis Synchronous Reactance
xdp	0.30	Direct Axis Transient Reactance
Td0p	7	Open-circuit Direct Axis Transient Time Constant
Ef0	1.72250079258051
Efmax	2.2
Pm0	0.352
Pmmax	1
wref	1

Modelica definition

model GenQSS "Quasi-Steady State Model of a generator" 
  extends Basic.OnePin;
  // typical limits for terminal variables
  // T.ia(min=-1.05, max=1.05), T.ib(min=-1.05, max=1.05)
  // T.va(min=-0.5, max=0.5  ), T.vb(min=-0.5,  max=0.5)
  parameter Real H(
    min=0.1, 
    max=20) = 3 "Inertia Constant";
  parameter Real D(
    min=0, 
    max=20) = 0 "Damping Coefficient";
  parameter Real ra(
    min=0.0, 
    max=0.02) = 0 "Armature Resistance";
  parameter Real xd(
    min=0.6, 
    max=2.4) = 0.8948 "Direct Axis Synchronous Reactance";
  parameter Real xq(
    min=0.4, 
    max=2.4) = 0.84 "Quadrature Axis Synchronous Reactance";
  parameter Real xdp(
    min=0.15, 
    max=1) = 0.30 "Direct Axis Transient Reactance";
  parameter Real Td0p(
    min=1.5, 
    max=10) = 7 "Open-circuit Direct Axis Transient Time Constant";
  
  parameter Real Ef0(
    min=1.5, 
    max=9) = 1.72250079258051;
  parameter Real Efmax=2.2;
  
  parameter Real Pm0=0.352;
  parameter Real Pmmax=1;
  parameter Real wref=1;
  
  Real Eqp(
    start=1, 
    min=0, 
    max=2);
  Real w(
    start=1, 
    min=0.8, 
    max=1.2) "Angular Speed";
  Real delta(min=-Modelica.Constants.PI/2, max=Modelica.Constants.PI/2);
  
  Real id(min=-1.2, max=1.2);
  Real iq(min=-1.2, max=1.2);
  Real vd(min=-1.2, max=1.2);
  Real vq(min=-1.2, max=1.2);
  Real Pe(min=0, max=1.05);
  
  Real Efd(min=0, max=7);
  Real Pm(min=0, max=1.05);
  
equation 
  //   swing equations
  0 = 1/(2*H)*(Pm - Pe - D*(w - 1));
  0 = 2*Modelica.Constants.PI*(w - 1);
  
  // Transient EMF equation
  Eqp = (Efd + id*(xd - xdp));
  
  // stator equations
  vd = -ra*id - xq*iq;
  vq = Eqp + xdp*id - ra*iq;
  
  // electrical power
  Pe = Eqp*iq + (xdp - xq)*id*iq;
  
  // coordinate change
  -T.ia = -sin(delta)*id + cos(delta)*iq;
  -T.ib = cos(delta)*id + sin(delta)*iq;
  1 + T.va = -sin(delta)*vd + cos(delta)*vq;
  T.vb = cos(delta)*vd + sin(delta)*vq;
end GenQSS;

ABB_CC_Testcase.Components.Transformer

Information

The tap changer controller is modelled as a state automata.

Parameters

Name	Default	Description
R	0.0	Leakage Resistance
X	0.1	Leakage Reactance
stepsize	0.02

Modelica definition

model Transformer "Transformer with Voltage Controller " 
  extends ImpTransformer;
  
  parameter Real stepsize=0.02;
  Integer tappos;
equation 
  Tr.n = 1 + stepsize*tappos;
end Transformer;

ABB_CC_Testcase.Components.Varimp

Parameters

Name	Default	Description
R	0.0	Resistance

Modelica definition

class Varimp 
  extends Basic.TwoPin;
  
  parameter Real R=0.0 "Resistance";
  
  input Real X "Reactance";
equation 
  [T1.va - T2.va; T1.vb - T2.vb] = [R, -X; X, R]*[T1.ia; T1.ib];
  [T1.ia; T1.ib] + [T2.ia; T2.ib] = [0; 0];
end Varimp;

ABB_CC_Testcase.Components.Capacitor

Parameters

Name	Default	Description
G	0
B	0.1

Modelica definition

class Capacitor 
  extends Basic.OnePin;
  
  parameter Real G=0;
  parameter Real B=0.1;
  discrete input Integer step(min=0, max=3);
  
equation 
  [T.ia; T.ib] = step*[G, -B; B, G]*[1 + T.va; T.vb];
  
end Capacitor;

ABB_CC_Testcase.Components.IdealTransformer

Modelica definition

model IdealTransformer 
  extends Basic.TwoPin;
  Real n(start=1);
  Modelica.Blocks.Interfaces.InPort inPort(final n=1);
equation 
  (1 + T1.va)*n = 1 + T2.va;
  T1.vb*n = T2.vb;
  T1.ia = -T2.ia*n;
  T1.ib = -T2.ib*n;
  n = inPort.signal[1];
end IdealTransformer;

ABB_CC_Testcase.Components.ImpTransformer

Parameters

Name	Default	Description
R	0.0	Leakage Resistance
X	0.1	Leakage Reactance

Modelica definition

partial model ImpTransformer 
  extends Basic.TwoPin;
  parameter Real R=0.0 "Leakage Resistance";
  parameter Real X=0.1 "Leakage Reactance";
  IdealTransformer Tr;
  Impedance Imp(R=R, X=X);
equation 
  connect(Imp.T1, T1);
  connect(Imp.T2, Tr.T1);
  connect(Tr.T2, T2);
end ImpTransformer;

ABB_CC_Testcase.Components.Bus

Modelica definition

model Bus "Busbar model" 
  extends Basic.OnePinCenter;
  Real V;
  Real theta;
equation 
  T.ia = 0;
  T.ib = 0;
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
  theta = Modelica.Math.atan2(T.vb, (1 + T.va));
end Bus;

ABB_CC_Testcase.Components.Impedance

Information

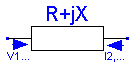
The impedance model is governed by the equations:
           R+jX
           ----
V1, I1  ---    --- V2, I2
    ->     ----        <-
V1 - V2 = (R+jX) * I1
I1 + I2 = 0:
For numerical reasons, R and X may not both be set to zero.

Parameters

Name	Default	Description
R	0.0	Resistance
X	0.1	Reactance

Modelica definition

model Impedance "Impedance model" 
  extends Basic.TwoPin;
  
  parameter Real R=0.0 "Resistance";
  parameter Real X=0.1 "Reactance";
  
equation 
  
  [T1.va - T2.va; T1.vb - T2.vb] = [R, -X; X, R]*[T1.ia; T1.ib];
  [T1.ia; T1.ib] + [T2.ia; T2.ib] = [0; 0];
end Impedance;

ABB_CC_Testcase.Components.Pilink

Parameters

Name	Default	Description
R	0.0	Resistance
X	0.1	Reactance
B	0.1	Shunt Susceptance
G	0.0	Shunt Conductance

Modelica definition

model Pilink "Pilink Line Model" 
  extends Basic.TwoPin;
  
  parameter Real R=0.0 "Resistance";
  parameter Real X=0.1 "Reactance";
  parameter Real B=0.1 "Shunt Susceptance";
  parameter Real G=0.0 "Shunt Conductance";
equation 
  [T1.ia; T1.ib] = [G, -B; B, G]/2*[1 + T1.va; T1.vb] + [R, X; -X, R]/(R^2 + X^
    2)*[T1.va - T2.va; T1.vb - T2.vb];
  [T2.ia; T2.ib] = [G, -B; B, G]/2*[1 + T2.va; T2.vb] - [R, X; -X, R]/(R^2 + X^
    2)*[T1.va - T2.va; T1.vb - T2.vb];
  
end Pilink;

ABB_CC_Testcase.Components.GenQSS2

Parameters

Name	Default	Description
H	3	Inertia Constant
D	0	Damping Coefficient
ra	0	Armature Resistance
xd	0.8948	Direct Axis Synchronous Reactance
xq	0.84	Quadrature Axis Synchronous Reactance
xdp	0.30	Direct Axis Transient Reactance
Td0p	7	Open-circuit Direct Axis Transient Time Constant
Pm0	0.352

Modelica definition

model GenQSS2 "Quasi-Steady State Model of a generator" 
  extends Basic.OnePin;
  parameter Real H=3 "Inertia Constant";
  parameter Real D=0 "Damping Coefficient";
  parameter Real ra=0 "Armature Resistance";
  parameter Real xd=0.8948 "Direct Axis Synchronous Reactance";
  parameter Real xq=0.84 "Quadrature Axis Synchronous Reactance";
  parameter Real xdp=0.30 "Direct Axis Transient Reactance";
  parameter Real Td0p=7 "Open-circuit Direct Axis Transient Time Constant";
  
  Real Pg;
  Real Qg;
  
  Real Efd;
  Real V;
  parameter Real Pm0=0.352;
  
equation 
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
  Efd = (V^4 + V^2*Qg*xq + Qg*xd*V^2 + Qg^2*xd*xq + Pg^2*xq*xd)/(sqrt(Pg^2*xq^2
     + V^4 + 2*V^2*Qg*xq + Qg^2*xq^2)*V);
  Pg = Pm0;
  Pg = -((1 + T.va)*T.ia + T.vb*T.ib);
  Qg = -(T.vb*T.ia - (1 + T.va)*T.ib);
end GenQSS2;

ABB_CC_Testcase.Components.FixCapacitor

Parameters

Name	Default	Description
G	0
B	0.1

Modelica definition

class FixCapacitor 
  extends Basic.OnePin;
  
  parameter Real G=0;
  parameter Real B=0.1;
equation 
  [T.ia; T.ib] = [G, -B; B, G]*[1 + T.va; T.vb];
end FixCapacitor;

ABB_CC_Testcase.Components.FixTransformer

Parameters

Name	Default	Description
R	0.0	Leakage Resistance
X	0.1	Leakage Reactance
n	1	Transformer Ratio [p.u.]

Modelica definition

model FixTransformer "Fixed Ratio Transformer" 
  extends ImpTransformer;
  parameter ObjectStab.Base.TapRatio n=1 "Transformer Ratio";
equation 
  Tr.n = n;
end FixTransformer;

ABB_CC_Testcase.Components.LinearRecoveryLoad

Information

Linear recovery load

Parameters

Name	Default	Description
P0	.1	Rated Active Power Load
Q0	.02	Rated Reactive Power Load
kp	10
kq	10
Tp	60	Active power recovery time constant
Tq	60	Reactive power recovery time constant
ShedStep	0.05

Modelica definition

model LinearRecoveryLoad "Dynamic exponential recovery load" 
  extends Basic.OnePin;
  parameter Real P0=.1 "Rated Active Power Load";
  parameter Real Q0=.02 "Rated Reactive Power Load";
  parameter Real kp=10;
  parameter Real kq=10;
  parameter Real Tp=60 "Active power recovery time constant";
  parameter Real Tq=60 "Reactive power recovery time constant";
  parameter Real ShedStep=0.05;
  discrete input Integer step(min=0, max=3) "Load Shedding Constant";
  Real G;
  Real B;
  Real V;
  Real Pl;
  Real Ql;
  discrete Real G0;
  discrete Real B0;
equation 
  Pl = ((1 + T.va)*T.ia + T.vb*T.ib);
  Ql = (T.vb*T.ia - (1 + T.va)*T.ib);
  
  Tp*der(G) + G = -kp*(Pl - P0) + G0;
  Tq*der(B) + B = kq*(Ql - Q0) + B0;
  
  [T.ia; T.ib] = (1 - step*ShedStep)*[G, -B; B, G]*[1 + T.va; T.vb];
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
  G0 = pre(G0);
  B0 = pre(B0);
initial equation 
  Pl = P0;
  Ql = Q0;
  der(G) = 0;
  der(B) = 0;
end LinearRecoveryLoad;

ABB_CC_Testcase.Components.ParTripLine

Parameters

Name	Default	Description
R	0.0	Resistance (per line)
X	0.8	Reactance (per line)
no	2	total no of lines

Modelica definition

class ParTripLine 
  extends Basic.TwoPin;
  
  parameter Real R=0.0 "Resistance (per line)";
  parameter Real X=0.8 "Reactance (per line)";
  
  parameter Integer no=2 "total no of lines";
  input Integer faulted "no of tripped ines";
equation 
  if (no - faulted) == 0 then
    [T1.ia; T1.ib] = [0; 0];
  else
    [T1.va - T2.va; T1.vb - T2.vb] = [R, -X; X, R]/(no - faulted)*[T1.ia; T1.ib];
  end if;
  [T1.ia; T1.ib] + [T2.ia; T2.ib] = [0; 0];
end ParTripLine;

ABB_CC_Testcase.Components.SimplerLoad

Information

Dynamic exponential recovery load according to Karlsson 
The load powers are given by:
  der(xp) = P0*(V^(as) - V^at) - xp/Tp;
  Pl = (xp/Tp + P0*V^at);
  der(xq) = Q0*(V^(bs) - V^bt) - xq/Tq;
  Ql = (xq/Tq + Q0*V^bt);
where xp is a continuous dynamic state that can be interpreted as a
measure of the energy deficit in the load and Ps(V) = P0*V^as 
is the steady-state and Pt(V)=P0*V^at the transient voltage dependency.
Pl is the actual active load power and Tp is the active power recovery 
time constant. 
For the reactive load power, a similar model is used with corresponding 
characteristics x_q, Qs(V)=Q0 V^bs, Qt(V) = Q0 V^bt and time constant Tq.
---
[1] D. Karlsson and D.J. Hill, "Modelling and identification of nonlinear 
dynamic loads in power systems", IEEE Transactions on Power Systems, 
vol. 9, no. 1, pp. 157-163, February 1994.

Parameters

Name	Default	Description
xp0	0	Initial Value for xp
as	0.5	Steady-state voltage dependency
at	2	Transient voltage dependency
P0	.1	Rated Active Power Load
Q0	.02	Rated Reactive Power Load
Tp	60	Recovery time constant
ShedStep	0.05

Modelica definition

model SimplerLoad "ZIP recovery load" 
  extends Basic.OnePin;
  parameter Real xp0=0 "Initial Value for xp";
  parameter Real as=0.5 "Steady-state voltage dependency";
  parameter Real at=2 "Transient voltage dependency";
  parameter Real P0=.1 "Rated Active Power Load";
  parameter Real Q0=.02 "Rated Reactive Power Load";
  parameter Real Tp=60 "Recovery time constant";
  parameter Real ShedStep=0.05;
  discrete input Integer step(min=0, max=3) "Load Shedding Constant";
  Real xp(
    min=-1, 
    max=1, 
    start=xp0, 
    fixed=true) "Internal Load State";
  Real V;
  Real Pl;
  Real Ql;
equation 
  Pl = (1 - step*ShedStep)*(xp/Tp + P0*V^2);
  Ql = Pl*Q0/P0;
  der(xp) = P0*(V^as - V^at) - xp/Tp;
  
  T.ia = (T.vb*Ql + Pl + Pl*T.va)/(1 + 2*T.va + T.va*T.va + T.vb*T.vb);
  T.ib = (Pl*T.vb - Ql - T.va*Ql)/(1 + 2*T.va + T.va*T.va + T.vb*T.vb);
  V = sqrt((1 + T.va)*(1 + T.va) + T.vb*T.vb);
end SimplerLoad;

ABB_CC_Testcase.Components.DBControl

Parameters

Name	Default	Description
idle0[3]	{false,false,false}
wait0[3]	{true,true,true}
action0[3]	{false,false,false}
pos0[3]	{-1,3,3}
timer0[3]	{0,0,0}
Delay[3]	{30,30,30}
MechDelay[3]	{1,1,1}
DB[3]	{0.01*3,0.01*3,0.01*3}
Max[3]	{10,10,10}
Min[3]	{-10,-10,-10}

Modelica definition

model DBControl "Integral controller with Deadband" 
  parameter Boolean idle0[3]={false,false,false};
  parameter Boolean wait0[3]={true,true,true};
  parameter Boolean action0[3]={false,false,false};
  parameter Integer pos0[3]={-1,3,3};
  parameter Real timer0[3]={0,0,0};
  
  input Real Vref[3];
  parameter Real Delay[3]={30,30,30};
  parameter Real MechDelay[3]={1,1,1};
  parameter Real DB[3]={0.01*3,0.01*3,0.01*3};
  parameter Real Max[3]={10,10,10};
  parameter Real Min[3]={-10,-10,-10};
  
  Boolean idle[3](start=idle0, fixed=true);
  Boolean wait[3](start=wait0, fixed=true);
  Boolean action[3](start=action0, fixed=true);
  Integer pos[3](start=pos0, fixed=true);
  Real timer[3](start=timer0, fixed=true);
  Boolean toohigh[3];
  Boolean toolow[3];
  
  input Real u[3];
  output Integer y[3];
equation 
  // tap changer control - state automata !
  for k in 1:3 loop
    toohigh[k] = (u[k] - Vref[k]) > DB[k]/2;
    toolow[k] = (u[k] - Vref[k]) < -DB[k]/2;
    idle[k] = (pre(idle[k]) or pre(wait[k])) and not (pre(toohigh[k]) or pre(
      toolow[k])) or (pre(action[k]) and ((time - timer[k]) > Delay[k] + 
      MechDelay[k]));
    wait[k] = (pre(idle[k]) and (pre(toohigh[k]) or pre(toolow[k]))) or pre(
      wait[k]) and ((pre(toolow[k]) or pre(toohigh[k])) and ((time - pre(timer[
      k])) < Delay[k]));
    action[k] = (pre(wait[k]) and (time - timer[k] > Delay[k])) or pre(action[k])
       and ((time - timer[k]) < Delay[k] + MechDelay[k]);
    
    when wait[k] and not pre(wait[k]) and not initial() then
      timer[k] = time;
    end when;
    
    when pre(action[k]) and not action[k] then
      if pre(toolow[k]) and (pre(pos[k]) < Max[k]) then
        pos[k] = pre(pos[k]) + 1;
      elseif pre(toohigh[k]) and (pre(pos[k]) > Min[k]) then
        pos[k] = pre(pos[k]) - 1;
      else
        pos[k] = pre(pos[k]);
      end if;
    end when;
    y[k] = pos[k];
    
  end for;
end DBControl;