ABB_CC_Testcase.Fournode

Information

Small scale benchmark system

Name	Description
OpenLoop	Open loop power system
PrimaryController	Primary Control System
PrimaryControlledSystem	Test case power system with example primary controls applied
ClosedLoop	Test case power system with example emergency control applied

ABB_CC_Testcase.Fournode.OpenLoop

Information

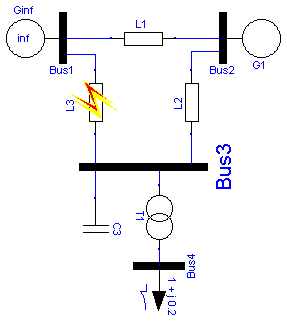
Test case power system without primary controls is a nonlinear 
system with pure continuous dynamics. 
The open loop power system has four control inputs:
CapStep 
  Nr of capacitor steps connected at bus 3
  can assume the values [0,1,2,3]. Each step corresponds
  to 0.1 p.u. of compensation.
LoadStep
  The nr of load shedding steps used at bus 4
  can assume the values [0,1,2,3]. Each step corresponds
TrStep
   The position of the tap changer on transformer T1
G1Efd
   The field voltage of generator G1
 
The test case has one disturbance input:
  
faulted
   Boolean variable indicating whether or not line L3 is faulted.
   The fault is modelled by the change of the impedance of the line
   from 1 p.u. to 1.5 p.u. 
  
The open loop power system has three controlled outputs:
V2,V3,V4
   The voltage at buses 2,3 and 4 respectively.
   The aim of emergency control is to keep the voltages 
   V2,V3,V4 within the limits [0.9 p.u. and 1.1 p.u.] despite
   the fault input becoming true. 
Additionally the two dynamic states has bee included as auxilliary outputs:
xp,xq 
   The two dynamic state variables
        
Recommended initial input values are:
CapStep=2, LoadStep=0, TrStep=1, and faulted=false (0)

Parameters

Name	Default	Description
L3X_1	0.5
L3X_2	1.5
SimulinkSafe	true
G1	redeclare Components.GenQSS2 G1(xd=2.38, xq=2.27, xdp=0.91, Td0p=9.6)

Modelica definition

model OpenLoop "Open loop power system" 
  parameter Real L3X_1=0.5;
  parameter Real L3X_2=1.5;
  
  input Integer CapStep;
  input Integer LoadStep;
  input Integer TrStep(start=1);
  input Real G1Efd;
  input Boolean faulted;
  
  output Real V2;
  output Real V3;
  output Real V4;
  output Real xp;
  output Real xq;
  parameter Boolean SimulinkSafe=true;
protected 
  constant Real Ef0=1.55;
public 
  Components.Transformer T1(X=0.0031);
  Components.Capacitor C3;
  Components.Varimp L3;
  Components.Bus Bus1;
  Components.Bus Bus2;
  Components.Bus Bus3;
  Components.Bus Bus4;
  Components.Slack Ginf(V0=1.03);
  Components.Impedance L1(X=0.75);
  Components.Impedance L2(X=0.7);
  Components.Load Load(
    P0=1, 
    Q0=0.2, 
    as=0, 
    at=2, 
    bs=1, 
    bt=2);
  replaceable Components.GenQSS2 G1(
    xd=2.38, 
    xq=2.27, 
    xdp=0.91, 
    Td0p=9.6);
equation 
  connect(Bus4.T, T1.T2);
  connect(C3.T, Bus3.T);
  connect(T1.T1, Bus3.T);
  connect(L3.T1, Bus3.T);
  connect(L2.T1, Bus3.T);
  connect(Bus1.T, Ginf.T);
  connect(L1.T2, Bus2.T);
  connect(Bus2.T, L2.T2);
  connect(L3.T2, Ginf.T);
  connect(Ginf.T, L1.T1);
  connect(Load.T, Bus4.T);
  connect(Bus2.T, G1.T);
  
  if SimulinkSafe then
    G1.Efd = if noEvent(abs(G1Efd) > 1e-5) then G1Efd else Ef0;
  else
    G1.Efd = G1Efd;
  end if;
  C3.step = CapStep;
  Load.step = LoadStep;
  T1.tappos = TrStep;
  
  V2 = Bus2.V;
  V3 = Bus3.V;
  V4 = Bus4.V;
  xp = Load.xp;
  xq = Load.xp;
  
  L3.X = if faulted then L3X_2 else L3X_1;
end OpenLoop;

ABB_CC_Testcase.Fournode.PrimaryController

Information

This model models the primary control systems of the 
four node power system. 
It contains a tap changer controller for transformer T1
modelled as a state machine and an automatic voltage regulator
with filed voltage limiter modelled by a state machina and a linear 
control law.
The special equations activated by the flag SimulinkSafe
flag are just fixes that must be applied to make the model simulable with
Simulink. If you remodel this system with other tools,
use the original equations (assume that SimulinkSafe=false)

Parameters

Name	Default	Description
idle0	false
wait0	true
action0	false
tappos0	1
timer0	0
up_limit0	false
G1Vref	1.03
Ef0	1.55
Efmax	2.2
TapDelay	30
MechDelay	1
TapDB	0.01*3
MaxTap	10
MinTap	-10
SimulinkSafe	true

Modelica definition

model PrimaryController "Primary Control System" 
  parameter Boolean idle0=false;
  parameter Boolean wait0=true;
  parameter Boolean action0=false;
  parameter Integer tappos0=1;
  parameter Real timer0=0;
  parameter Boolean up_limit0=false;
  
  input Real TapVref(start=1);
  input Real V2(start=1);
  input Real V3(start=1);
  input Real V4(start=1);
  
  Boolean idle(start=idle0, fixed=true);
  Boolean wait(start=wait0, fixed=true);
  Boolean action(start=action0, fixed=true);
  Integer tappos(start=tappos0, fixed=true);
  Real timer(start=timer0, fixed=true);
  Boolean up_limit(start=up_limit0, fixed=true);
  
  Boolean toohigh;
  Boolean toolow;
  
  output Real G1Efd;
  output Integer T1tappos;
  
  parameter Real G1Vref=1.03;
  parameter Real Ef0(
    min=1.5, 
    max=9) = 1.55;
  parameter Real Efmax=2.2;
  parameter Real TapDelay=30;
  parameter Real MechDelay=1;
  parameter Real TapDB=0.01*3;
  parameter Real MaxTap=10;
  parameter Real MinTap=-10;
  
  Real Efd(start=1.55);
  parameter Boolean SimulinkSafe=true;
equation 
  // generator voltage control
  if SimulinkSafe then
    0.01*der(Efd) + Efd = if up_limit then Efmax else Ef0 + (G1Vref - V2)*50;
  else
    Efd = if up_limit then Efmax else Ef0 + (G1Vref - V2)*50;
  end if;
  
  T1tappos = pre(tappos);
  G1Efd = Efd;
  // tap changer control - state automata !
  toohigh = (V4 - TapVref) > TapDB/2;
  toolow = (V4 - TapVref) < -TapDB/2;
  
  idle = (pre(idle) or pre(wait)) and not (toohigh or toolow) or (pre(action)
     and ((time - timer) > TapDelay + MechDelay));
  wait = (pre(idle) and (toohigh or toolow)) or pre(wait) and ((toolow or 
    toohigh) and ((time - pre(timer)) < TapDelay));
  action = (pre(wait) and (time - timer > TapDelay)) or pre(action) and ((time
     - timer) < TapDelay + MechDelay);
  up_limit = if not (pre(up_limit)) then (Efd > Efmax) else not (V2 > G1Vref);
  when wait and not pre(wait) and not initial() then
    timer = time;
  end when;
  when pre(action) and not action then
    if toolow and (pre(tappos) < MaxTap) then
      tappos = pre(tappos) + 1;
    elseif toohigh and (pre(T1tappos) > MinTap) then
      tappos = pre(tappos) - 1;
    else
      tappos = pre(tappos);
    end if;
  end when;
  
end PrimaryController;

ABB_CC_Testcase.Fournode.PrimaryControlledSystem

Parameters

Name	Default	Description
SimulinkSafe	false

Modelica definition

model PrimaryControlledSystem 
  "Test case power system with example primary controls applied" 
  input Integer CapStep;
  input Integer LoadStep;
  input Real TapVref;
  input Boolean faulted;
  output Real V2;
  output Real V3;
  output Real V4;
  output Real G1Efd;
  parameter Boolean SimulinkSafe=false;
  
  // auxilliary  outputs 
  output Real U1d;
  output Real U1q;
  output Real U2d;
  output Real U2q;
  output Real U3d;
  output Real U3q;
  output Real U4d;
  output Real U4q;
  
  output Real I1d;
  output Real I1q;
  output Real I2d;
  output Real I2q;
  output Real I3d;
  output Real I3q;
  output Real I4d;
  output Real I4q;
  output Real I5d;
  output Real I5q;
  output Real Icd;
  output Real Icq;
  
  output Real U2m;
  output Real U4m;
  output Real U4m2;
  output Real Efd;
  output Real P5l;
  output Real Q5l;
  
  output Integer T1_tappos;
  output Real T1_timer;
  output Real Load_xp;
  output Real Load_xq;
  output Boolean T1_idle;
  output Boolean T1_wait;
  output Boolean T1_action;
  output Boolean G1_up_limit;
  OpenLoop System(SimulinkSafe=SimulinkSafe);
  PrimaryController Controller(Ef0=1.54, SimulinkSafe=SimulinkSafe);
equation 
  V2 = System.V2;
  V3 = System.V3;
  V4 = System.V4;
  G1Efd = Controller.G1Efd;
  Controller.TapVref = TapVref;
  System.LoadStep = LoadStep;
  System.CapStep = CapStep;
  Controller.V2 = System.V2;
  Controller.V3 = System.V3;
  Controller.V4 = System.V4;
  System.G1Efd = Controller.G1Efd;
  System.TrStep = Controller.T1tappos;
  System.faulted = faulted;
  U1d = System.Bus1.T.va;
  U1q = System.Bus1.T.vb;
  U2d = System.Bus2.T.va;
  U2q = System.Bus2.T.vb;
  U3d = System.Bus3.T.va;
  U3q = System.Bus3.T.vb;
  U4d = System.Bus4.T.va;
  U4q = System.Bus4.T.vb;
  
  I1d = System.Ginf.T.ia;
  I1q = System.Ginf.T.ib;
  I2d = System.G1.T.ia;
  I2q = System.G1.T.ib;
  I3d = System.T1.T1.ia;
  I3q = System.T1.T1.ib;
  I4d = System.T1.T2.ia;
  I4q = System.T1.T2.ib;
  I5d = System.Load.T.ia;
  I5q = System.Load.T.ib;
  Icd = System.C3.T.ia;
  Icq = System.C3.T.ib;
  
  U2m = System.Bus2.V;
  U4m = System.Bus4.V;
  U4m2 = System.Bus4.V^2;
  Efd = System.G1.Efd;
  P5l = System.Load.Pl;
  Q5l = System.Load.Ql;
  
  T1_tappos = Controller.tappos;
  T1_timer = Controller.timer;
  Load_xp = System.Load.xp;
  Load_xq = System.Load.xq;
  T1_idle = Controller.idle;
  T1_wait = Controller.wait;
  T1_action = Controller.action;
  G1_up_limit = Controller.up_limit;
  
end PrimaryControlledSystem;

ABB_CC_Testcase.Fournode.ClosedLoop

Information

This model illustrates three possibilities of
emergency control. The aim of the emergeny control is
to stabilize the voltage of Bus 4 at a value higher than 0.9 
p.u.
It is trivial to design emergency control strategies
that will arrest the voltage collapse for a simple
with this simple structure based on heuristics.
strategy=0:
No emergency control, the voltage collapses after 568.5.
strategy=1:
Attempt to stabilize by change of transformer voltage control
setpoint, 
strategy=2:
Stabilitation by capacitor switching
strategy=3:
Stabilization by capacitor swithcing and tap reference
change
strategy=4:
Stabilization by load shedding

Parameters

Name	Default	Description
strategy	3
FaultTime	100
TimeOfControl	110

Modelica definition

model ClosedLoop 
  "Test case power system with example emergency control applied" 
  
  parameter Integer strategy=3;
  parameter Real FaultTime=100;
  parameter Real TimeOfControl=110;
  output Real V2;
  output Real V3;
  output Real V4;
  output Real Efd;
  ABB_CC_Testcase.Fournode.PrimaryControlledSystem PCS;
equation 
  // control strategy
  if strategy == 0 then
    // no emergency control
    PCS.TapVref = 1;
    PCS.CapStep = 2;
    PCS.LoadStep = 0;
  elseif strategy == 1 then
    //attempt to stabilize by tap reference change
    PCS.TapVref = if time > TimeOfControl then 0.92 else 1;
    PCS.CapStep = 2;
    PCS.LoadStep = 0;
  elseif strategy == 2 then
    //attempt to stabilize by cap switching
    PCS.TapVref = 1;
    PCS.CapStep = if time > TimeOfControl then 3 else 2;
    PCS.LoadStep = 0;
  elseif strategy == 3 then
    //succesful stabilization by cap switching and tap reference change
    PCS.TapVref = if time > TimeOfControl then 0.92 else 1;
    PCS.CapStep = if time > TimeOfControl then 3 else 2;
    PCS.LoadStep = 0;
  elseif strategy == 4 then
    // stabilization by load shedding
    PCS.TapVref = 1;
    PCS.CapStep = 2;
    PCS.LoadStep = if time > TimeOfControl then 3 else 0;
  end if;
  PCS.faulted = if time > FaultTime then true else false;
  V2 = PCS.System.V2;
  V3 = PCS.System.V3;
  V4 = PCS.System.V4;
  Efd = PCS.Controller.Efd;
end ClosedLoop;