Wide DHMPC DMPCC
Contents |
Decentralized Linear Model Predictive Control
The class Decentralized LINear CONstrained (dlincon) is an extension of the object lincon from Hybrid toolbox (by A. Bemporad) which allows to easily handle a set of decentralized linear MPC controllers. Moreover the a-posteriori stability test described in "Barcelli and Bemporad Decentralized Model Predictive Control of Dynamically-Coupled Linear Systems: Tracking under Packet Loss". Below we briefly recall the basic concepts of that contribution so as to describe the trems of applicability.
Problem Setup
Consider the problem of regulating the discrete-time linear time-invariant system
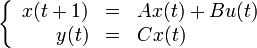
to the origin while fulfilling the constraints
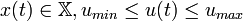
at all time instants 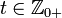 , where
, where 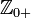 is the set of nonnegative integers,
is the set of nonnegative integers, 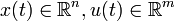 and
and 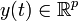 are the state, input, and output vectors, and the pair (A,B) is stabilizable.
are the state, input, and output vectors, and the pair (A,B) is stabilizable.
Assumption 1: Matrix A has all its eigenvalues strictly inside the unit disc.
The Assumption 1 restricts the strategy and stability results to processes that are open-loop asymptotically stable, leaving to the controller the mere role of optimizing the performance of the closed-loop system.
Consider the following finite-horizon optimal control problem:
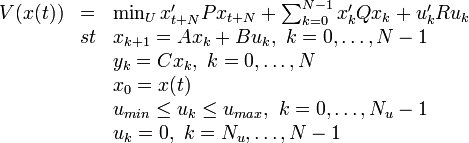
where, at each time t, 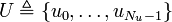 is the sequence of future input moves, xk denotes the predicted state vector at time t + k, obtained by applying the input sequence
is the sequence of future input moves, xk denotes the predicted state vector at time t + k, obtained by applying the input sequence 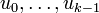 to the model, starting from x(t).
N > 0 is the prediction horizon,
to the model, starting from x(t).
N > 0 is the prediction horizon, 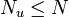 is the input horizon, and "
is the input horizon, and "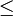 " denotes component-wise inequalities.
We assume that
" denotes component-wise inequalities.
We assume that 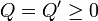 , R = R' > 0,
, R = R' > 0, 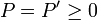 are square weight matrices defining the performance index, and P solves the Lyapunov equation P = A'PA + Q.
are square weight matrices defining the performance index, and P solves the Lyapunov equation P = A'PA + Q.
Decentralized Prediction Models
In general the matrices A, B have a certain number of zero or negligible components corresponding to a partial dynamical decoupling of the process, or are even block diagonal in case of total dynamical decoupling.
Let M be the number of decentralized control actions that we want to design, for example M = m in case each individual actuator is governed by its own controller. For all 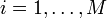 , we define
, we define 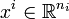 as the vector collecting a subset
as the vector collecting a subset 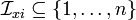 of the state components,
of the state components,
![x^i=W_i' x=\left[\begin{array}{ccc}x^{i}_1& \cdots & x^{i}_{n_i}\end{array}\right] ' \in \mathbb{R}^{n_i}](/HYCON2/images/math/1/0/f/10fe6a55e8b04772f9f8a5c1b2244dec.png)
where 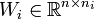 collects the ni columns of the identity matrix of order n corresponding to the indices in
collects the ni columns of the identity matrix of order n corresponding to the indices in 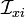 , and, similarly,
, and, similarly,
![u^i=Z_i' u=\left[\begin{array}{ccc}u^{i}_1& \cdots &u^{i}_{m_i}\end{array}\right] ' \in \mathbb{R}^{m_i}](/HYCON2/images/math/3/4/d/34defe2173f8b2f165aa9fade288cac0.png)
as the vector of input signals tackled by the i-th controller,
where 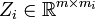 collects mi columns of the
identity matrix of order m corresponding to the set of indices
collects mi columns of the
identity matrix of order m corresponding to the set of indices
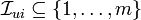 . Note that
. Note that
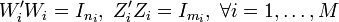
where 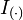 denotes the identity matrix of order
denotes the identity matrix of order 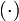 .
.
By definition of xi we obtain
xi(t + 1) = Wi'x(t + 1) = Wi'Ax(t) + Wi'Bu(t)
An approximation is obtained by changing Wi'A into Wi'AWiWi' and Wi'B into Wi'BZiZi', therefore getting the new prediction model of reduced order
xi(t + 1) = Aixi(t) + Biui(t)
where matrices 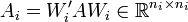 and
and 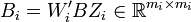 are submatrices of the original A and B matrices, respectively, describing in a possibly approximate way the evolution of the states of subsystem #i.
are submatrices of the original A and B matrices, respectively, describing in a possibly approximate way the evolution of the states of subsystem #i.
The choice of the pair (Wi,Zi) of decoupling matrices (and, consequently, of the dimensions ni, mi of each submodel) is a tuning knob of the DMPC procedure.
We want to design a controller for each set of moves ui according to the prediction model and based on feedback from xi, for all 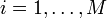 . Note that in general different states xi, xj and different ui, uj may share common components. To avoid ambiguities on the control action provided to the process, we impose that only a subset
. Note that in general different states xi, xj and different ui, uj may share common components. To avoid ambiguities on the control action provided to the process, we impose that only a subset 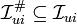 of input signals computed by controller #i is actually applied to the process without ambiguity, and for the sake of simplicity of notation since now on we assume that M = m, i.e., that controller #i only controls the ith input signal.
of input signals computed by controller #i is actually applied to the process without ambiguity, and for the sake of simplicity of notation since now on we assume that M = m, i.e., that controller #i only controls the ith input signal.
Decentralized Optimal Control Problems
Let the following assumption be satisfied:
Assumption 2: Matrix Ai has all its eigenvalues strictly inside the unit disc, 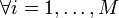 .
.
Assumption 2 restricts the degrees
of freedom in choosing the decentralized models (if Ai = A for all
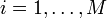 is the only choice satisfying Assumption 2,
then no decentralized MPC can be formulated within this framework).
For all
is the only choice satisfying Assumption 2,
then no decentralized MPC can be formulated within this framework).
For all 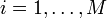 consider the following infinite-time
constrained optimal control problems
consider the following infinite-time
constrained optimal control problems
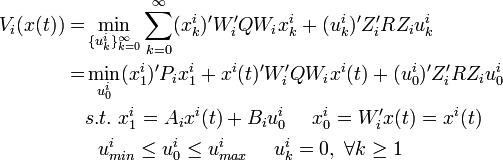
where 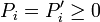 is the solution of the Lyapunov
equation
is the solution of the Lyapunov
equation
A'iPiAi − Pi = − W'iQWi
that exists by virtue of Assumption 2.
This latter problem corresponds to a finite-horizon constrained problem with control horizon Nu = 1 and linear stable prediction models. Note that only the local state vector xi(t) is needed to solve the problem.
Stability Test Under Packet Dropouts
Thereom 1:
Let N be a positive integer such that no more than N consecutive steps of channel
transmission blackout can occur. Assume u(t) = 0 is applied when no packet is received.
Let Assumptions 1,2 hold and 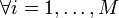 define
define
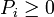 solution of A'iPiAi − Pi = − W'iQWi for
solution of A'iPiAi − Pi = − W'iQWi for 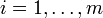
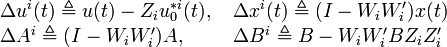
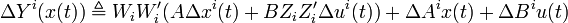
![\Delta S^i_j(x) \triangleq [2(A_iW_i'x+B_iu_0^{*i}(x))'W_i'+\Delta Y^i(x)'] (A^{j-1})'W_iP_iW_i' A^{j-1}\Delta Y^i(x)](/HYCON2/images/math/0/b/6/0b69472edf83fbfcbd22e1d6d72cff7f.png)
and let
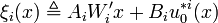 .
.
If the condition
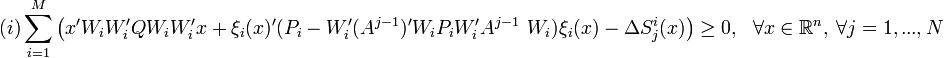
is satisfied, or the condition
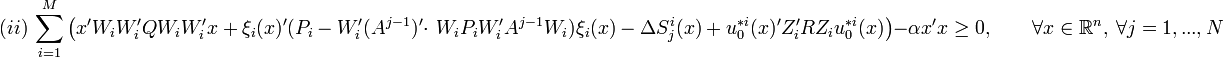
is satisfied for some scalar α > 0, then the decentralized MPC scheme in closed loop with the decentralized controller is globally asymptotically stable under packet loss.
Remark : Around the origin both the conditions in (i) and (ii) become a quadratic form to be checked positive semidefinite, so local stability in closed loop under packet loss can be tested for any arbitrary fixed N.
Class description
Starting with an user defined decentralization, the toolbox automatically creates the corresponding set of decentralized lincon controllers of appropriate dimension. The user is requested to provide a starting configuration for the centralized controller (using the same parameters as in in lincon) that is used to derive, accordingly with the given decentralization, a corresponding decentralized setup, i.e. configure each controller with corresponding state, input and output variables weights and constraints. Moreover each controller can easily be customized according to individual needing just as any lincon object.
Methods are available for three kinds of control action computation:
- global : centralized controller;
- Dglobal: run all DMPCs and assemble the components to return the complete set of inputs;
- i : run the i-th controller and return its results only;
Both regulator and tracking modes are supported, however the latter is realized by means of coordinates shift, as described in the paper. Classical tracking is currently under development.
Class Methods
Class constructor
dl = dlincon(model,type,cost,interval,limits,yzerocon,decent,varbounds);
model : centralized LTI model of the plant
type : 'reg' for regulator or 'track' for tracking
cost : structure with state and input matrices weights (see lincon for more details);
interval : structure with fields N and Nu, prediction and simulation horizons respectively (see lincon for more details);
limits : structure with bounds on states and inputs (see lincon for more details);
yzerocon : if 1 constraints are also enforced at the starting instant (see lincon for more details);
decent : decentralization structure, see Properties for a more detailed help;
varbounds : if 1 state are added to handle variant bounds specified by the user online to be enforced.
Optimal Input Computation
u = dl.Deval(type,xk,r) or u = Deval(dl,type,xk,r) where dl is a dlincon obj
type: global : centralized controller; Dglobal: run all DMPCs and assemble the components to output the complete set of inputs; i : run the i-th controller and outputs its results only;
xk : state measurements of estimations (must be coherent with state dimension
r : vector of references for the outputs, ignored if type='reg'.
Stability Test Around the Origin
ris=stability_test(dl,range,cost);
Returns the test outcome. Such sufficient only test is described in the paper.